Trong bài thi SAT Toán, có nhiều nội dung khá quen thuộc đối với học sinh THPT. Tuy nhiên, có một khía cạnh xem chừng lạ lẫm hơn, đó là “Data Analysis” – phân tích dữ liệu.
Bài viết hôm nay sẽ đi vào một nhánh nhỏ của nội dung này, đó là thống kê và xử lý số liệu, bên cạnh đó sẽ tập trung làm rõ đại lượng “Standard deviation” – độ lệch chuẩn.
Một số thuật ngữ trong bài
| data set | tập dữ liệu (thường là các số) |
| mean | giá trị trung bình |
| median | giá trị trung vị |
| mode | số yếu vị (số xuất hiện nhiều lần nhất) |
| outlier | điểm dữ liệu bất thường |
| range | khoảng biến thiên |
| standard deviation | độ lệch chuẩn |
| value | giá trị |
| frequency | tần số (số lần xuất hiện) |
| histogram | biểu đồ tần suất |
| dot plot | biểu đồ chấm (biểu đồ điểm) |
Thống kê, xử lý số liệu trong bài thi SAT Toán
Với những câu hỏi loại này, bạn sẽ được cung cấp một hoặc nhiều bảng số liệu, và câu hỏi sẽ xoay quanh các giá trị của bảng cũng như sự phân bố của chúng. Đối với sự phân bố, ta thường quan tâm đến hai điều: trung tâm (các giá trị chạy xung quanh điểm nào?), và độ rộng (các giá trị trải ra xa hay gần trung tâm?)
- Trung tâm của phân bố
Có 3 đại lượng thường được sử dụng trong đánh giá về trung tâm phân bố của các giá trị:
- Mean: Giá trị trung bình
Đối tượng này rất quen thuộc với chúng ta, chính là trung bình cộng của một tập hợp các số.
Ví dụ: Find the mean of the set {2, 7, 3, 1}
Giá trị trung bình (trung bình cộng) của tập hợp trên là
(2 + 7 + 4)/3 = 4.25
Chú ý: Theo quy ước quốc tế, phần thập phân được ngăn cách bởi dấu chấm.
- Medium: Số trung vị
Cái tên thể hiện trực tiếp ý nghĩa của đại lượng này. Trung vị được hiểu nôm na là “vị trí ở giữa”, do đó trong một dãy số, số trung vị được xác định bằng cách xếp dãy đã cho theo thứ tự tăng dần (hoặc giảm dần) rồi lấy giá trị ở vị trí chính giữa. Trong trường hợp, có một số chẵn các số trong tập, ta lấy trung bình cộng của hai số ở vị trí chính giữa.
Ví dụ 1.1:
Find the median of the set {2, 7, 3, 1}
- Sắp xếp các giá trị theo thứ tự tăng dần: 1, 2, 3, 7
- Hai số ở vị trí chính giữa là 2 và 3
- Số trung vị của tập này là (2 + 3)/2 = 2.5
Find the median of the set {12, 30, 17}
- Sắp xếp các giá trị theo thứ tự tăng dần: 12, 17, 30
- Số trung vị (chính là số ở vị trí chính giữa) của tập này là 17
Chú ý: Nếu các thao tác còn lại đều chính xác, thì giá trị thu được không phụ thuộc vào việc sắp xếp các giá trị theo thứ tự tăng hay giảm dần. Do đó trong thực hành, để tìm số trung vị chỉ cần sắp dãy theo một thứ tự xác định tuỳ ý.
- Mode: Số xuất hiện nhiều nhất trong tập số đã cho
Trong thống kê, “mode” còn được gọi là “số yếu vị”, tuy nhiên để tránh sự nhầm lẫn giữa các khái niệm, bạn chỉ cần nắm định nghĩa nêu trên.
Ví dụ 1.2: Find the mode of the set {2, 3, 3, 7, 9, 10}
Giá trị xuất hiện nhiều nhất trong tập trên là 3, nên đây cũng là “mode” của tập hợp số này.
Chú ý: Một tập hợp số có thể có nhiều “mode” (như {1, 1, 2, 2, 3, 3}), hoặc cũng có thể không có giá trị “mode” nào (như {1, 2, 3, 4, 5}).
Nhận xét: Trong các câu hỏi về thống kê, các giá trị đều đại diện cho một đơn vị nào đó (số giờ làm việc; chiều cao, cân nặng;…), và chúng thường được biểu diễn qua dạng bảng, biểu đồ. Nhiệm vụ của ta là xác định rõ đơn vị, hay đối tượng, được hỏi trong bài, qua đó xác định đúng những con số được đo lường kèm theo.
Trong các cách đánh giá về trung tâm của phân bố, “mean” và “median” được sử dụng thường xuyên hơn. Thoạt nhiên hai giá trị này có vẻ giống nhau, nhưng trong trường hợp xuất hiện các “điểm dữ liệu bất thường” (outliers) thì sự khác biệt giữa hai đại lượng này là rất đáng kể. Ví dụ sau vừa để thực hành các thao tác tính toán, vừa minh họa cho hiện tượng trên.
Ví dụ 1.3:
Đề bài:
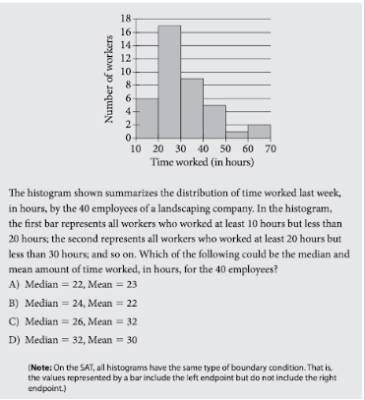
Biểu đồ tần suất trên ghi lại thời gian làm việc, tính theo giờ, của 40 nhân viên của một công ty về kiến trúc cảnh quan trong tuần vừa rồi. Trên bảng, cột thứ nhất (từ trái sang) biểu thị số nhân viên đã làm việc trong khoảng 10-20 giờ; cột thứ hai biểu thị số nhân viên đã làm trong khoảng 20-30 giờ; và cứ như vậy. Lựa chọn nào biểu thị số giờ làm việc trung bình và trung vị của 40 nhân viên này một cách hợp lý?
Lưu ý:
- Thời gian làm việc của các nhân viên được chia thành từng khoảng, chứ không nhận một giá trị cụ thể. Do đó, đề bài không hỏi tính toán chính xác các đối tượng, mà chỉ cho một ước lượng hợp lý.
- Đối với biểu đồ tần suất như trên, SAT Toán quy ước mỗi cột đại diện cho giá trị biên bên trái, không đại diện cho giá trị biên bên phải. (Ví dụ: cột thứ nhất đại diện cho số giờ làm việc lớn hơn hoặc bằng 10 và nhỏ hơn 20.)
Hướng dẫn:
- Giá trị trung bình
Đối với những khoảng giá trị như trong bài, ta có thể nghĩ tới hai đánh giá sau:
1.3.1. Tính chặn trên và chặn dưới của giá trị trung bình
- Tính chặn trên bằng cách quy thời gian từ mỗi khoảng về điểm cận trên của khoảng: đồng nhất các giá trị trong cột thứ nhất về 20, các giá trị trong cột thứ hai về 30, và cứ như vậy.
- Trung bình cộng của các giá trị đang xét là:
(6.20 + 17.30 + 9.40 + 5.50 + 1.60 + 2.70)/40 = 36
- Tương tự trên, ta tính chặn dưới của giá trị trung bình bằng việc đồng nhất các giá trị trong cột thứ nhất về 10, các giá trị trong cột thứ hai về 20, và cứ như vậy.
- Trung bình cộng của các giá trị này là:
(6.10 + 17.20 + 9.30 + 5.40 + 1.50 + 2.60)/40 = 26
Từ đây, ta có kết luận rằng giá trị trung bình hợp lý phải nằm trong khoảng 26-36, qua đó loại đi phương án A, B.
1.3.2. Tính “trung bình” của giá trị trung bình.
Bước 1:
- Thao tác ở đây cũng giống như trên, chỉ khác ở chỗ ta đồng nhất giá trị của mỗi khoảng về giá trị trung gian (ở cột thứ nhất là 15, cột thứ hai là 25, và tương tự.)
- Trung bình cộng của các giá trị này là:
(6.15 + 17.25 + 9.35 + 5.45 + 1.55 + 2.65)/40 = 30
(Thực chất là điểm ở giữa trong khoảng 26-36 mà ta đã giới hạn ở đánh giá 1.3.1)
Bước 2:
- Tới đây, ta ưu tiên chọn các phương án có giá trị trung bình gần 30 hơn.
- Giá trị trung vị
Đối với nhiều bảng dữ liệu, số giá trị sẽ tương đối lớn, và tất nhiên các giá trị sẽ không được liệt kê một cách đơn thuần (theo kiểu {1, 2, 3, 4}). Tuy nhiên, khi các giá trị nhiều, người thống kê sẽ cần phải sắp xếp nó theo một quy luật nhất quán, đa số là theo thứ tự tăng dần, như trong bài tập này.
Bước 3:
Khi đó dãy các giá trị đã được sắp thứ tự, nên ta tiếp tục tiến hành như sau:
- Xác định vị trí chính giữa (số thứ tự ở giữa) của tập hợp số. Ở đây có 40 số (là số chẵn) nên ta lấy hai vị trí ở giữa là 20, 21.
- Ta thấy cột đầu tiên bao gồm 6 giá trị đầu tiên của dãy, cột thứ hai bao gồm 17 giá trị tiếp theo. Tính đến thời điểm này đã có 23 giá trị, do đó số ở vị trí thứ 20, 21 đều nằm trong khoảng 20-30.
- Như vậy, giá trị trung vị là trung bình cộng của hai số trong khoảng 20-30, nên bản thân nó cũng nằm trong khoảng này.
Đối chiếu với các phương án đã cho, ta loại được phương án D.
Từ các đánh giá đã thực hiện, phương án phù hợp nhất là C.
Bình luận
Tới đây, ta cũng thấy được phần nào những sự chênh lệch có thể xảy ra cho “mean” và “median”. Một cách chính xác hơn, giá trị trung bình (“mean”) dễ bị ảnh hưởng khi trong bảng dữ liệu có một số các giá trị lớn hoặc nhỏ bất thường. Khi có các dữ liệu nhỏ bất thường thì “mean” có xu hướng nhỏ hơn “median”, và ngược lại. Trong ví dụ trên, ta thấy “mean” có xu hướng lớn hơn “median” bởi có một số công nhân có số giờ làm việc cao đột biến (50-70 giờ).
Ta vừa bàn luận một chút về các cách đánh giá trung tâm của sự phân bố giá trị trong một tập hợp các số. Thông qua định nghĩa đã có, càng nhiều kinh nghiệm trong thực hành sẽ càng giúp bạn vận dụng chủ động, linh hoạt cách thức xác định các đối tượng trên. Bây giờ ta chuyển sang khía cạnh thứ hai của sự phân bố, đó là độ “trải rộng” của các giá trị.
- Độ trải rộng của một phân bố.
Trong phần này, có hai đại lượng chủ yếu:
- Range: Khoảng biến thiên.
Cách đơn giản nhất để đánh giá độ rộng của một phân bố là thông qua khoảng biến thiên, hiệu của giá trị lớn nhất và nhỏ nhất trong tập hợp các số.
Ví dụ 2.1: Find the range of the set {3, 1, 4, 7, 10}
Khoảng biến thiên của tập hợp các số này là: 10 – 1 = 9
- Standard deviation: độ lệch chuẩn
Như đã đề cập ở trên, đây là đối tượng có phép tính rất phức tạp, và khi số giá trị tương đối nhiều thì biểu thức tính toán sẽ khá cồng kềnh. Vì lý do này, SAT Toán sẽ không yêu cầu ta tính độ lệch chuẩn của một bộ dữ liệu, thay vào đó họ kiểm tra cách hiểu về đại lượng này thông qua việc so sánh (dựa vào phân tích trực giác) độ lệch chuẩn giữa các tập hợp số.
Lưu ý:
Độ lệch chuẩn cũng có công thức tường minh để xác định, như các đại lượng khác. Công thức này sẽ được trình bày ngay sau đây, nhưng không phải để tính toán cụ thể, mà là để tạo cơ sở cho “phân tích trực giác” của chúng ta.
- Sâu hơn về độ lệch chuẩn
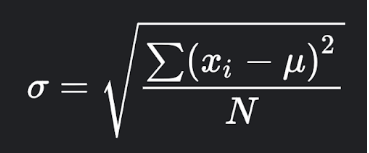
Công thức tính độ lệch chuẩn σ của một tập hợp gồm N giá trị
Hình trên là công thức tính độ lệch chuẩn σ của một tập hợp gồm N giá trị x1, x2,…, xN; với μ là giá trị trung bình của dãy.
Minh hoạ: Tính độ lệch chuẩn của tập {1, 2, 3, 4, 5, 6}
- Tìm giá trị trung bình: μ = (1 + 2 + 3 + 4 + 5 + 6)/6 = 3.5
- Tính từng “độ lệch” cụ thể:
- (1 – 3.5)2 = (6 – 3.5)2 = 6.25
- (2 – 3.5)2 = (5 – 3.5)2 = 2.25
- (3 – 3.5)2 = (4 – 3.5)2 = 0.25
- Đặt vào công thức của độ lệch chuẩn:
σ = (6.25 + 2.25 + 0.25 + 0.25 + 2.25 + 6.25)6 1.71
Nhận xét 2.2:
Các thao tác trên đủ cho thấy sự phức tạp trong việc tính độ lệch chuẩn, khi lượng dữ liệu tương đối lớn. Trong bài thi, việc làm này là không cần thiết, tuy nhiên công thức trên đã cho ta một chỉ dấu quan trọng để đánh giá đại lượng này, đó là độ gần/xa của các điểm dữ liệu so với giá trị trung bình của chúng.
Nhận xét 2.3:
Thông thường, SAT Toán chỉ hỏi về độ lệch chuẩn của một bộ dữ liệu khi chúng đã được thống kê qua một bảng tần số (như ở ví dụ 1.3). Khi này, ta có thể phán đoán rằng nếu các giá trị có xu hướng phân tán trên một phạm vi rộng thì độ lệch chuẩn của bộ dữ liệu này cao hơn, ngược lại nếu chúng có xu hướng co cụm về một khoảng giá trị nhất định thì độ lệch chuẩn sẽ thấp hơn.
Ta hãy làm rõ điều này qua các ví dụ sau:
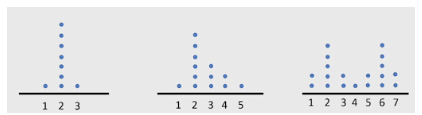
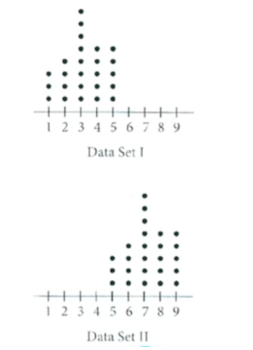
Ví dụ 2.4: Compare the standard deviations of the three dot plots shown.
 Hướng dẫn:
Hướng dẫn:
Từ nhận xét 2.2, 2.3, ta có:
– Bảng thứ nhất (ngoài cùng bên trái) có các giá trị tập trung lại rất dày quanh điểm 2, và dựa vào tính đối xứng thì 2 cũng là giá trị trung bình của tập hợp các số này. Ta tạm nói rằng độ lệch chuẩn của bảng này là “nhỏ” (“lớn, nhỏ” chỉ có nghĩa khi được đặt trong quan hệ so sánh).
– Bảng thứ hai có các giá trị tập trung nhiều ở 2, rồi đến 3, tuy nhiên bên cạnh đó là một số giá trị xa 2 hơn là 4 và 5. Tới đây ta khẳng định rằng độ lệch chuẩn của bảng hai lớn hơn bảng một.
– Cuối cùng tới bảng thứ ba. Ta thấy các giá trị ở đây trải rộng hơn hẳn hai bảng trước đó (từ 1-7), và dựa vào tính đối xứng ta thấy giá trị trung bình của bảng là 4. Vậy mà tuyệt đại đa số các điểm đều nằm khá xa so với 4, do đó ta khẳng định tập dữ liệu này có độ lệch chuẩn lớn nhất.
Kết luận: (độ lệch chuẩn của) bảng một < bảng hai < bảng ba.
Đây cũng sẽ là kết luận thu được nếu ta tính tường minh độ lệch chuẩn dựa vào công thức ở đầu mục.
Ví dụ 2.5:
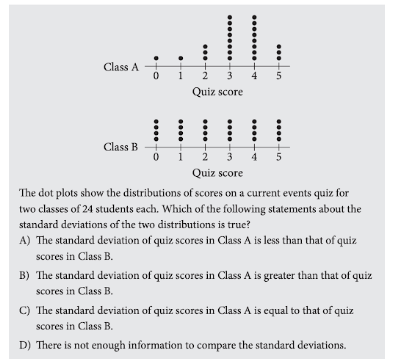
Đề bài: Biểu đồ chấm trên thể hiện điểm số trong một bài kiểm tra trắc nghiệm của hai lớp học, trong đó mỗi lớp có 24 học sinh. Khẳng định nào sau đây về độ lệch chuẩn của hai bộ dữ liệu là chính xác?
Hướng dẫn:
- Bảng A có các giá trị tập trung nhiều quanh 3, 4. Gần đó là các giá trị 2, 5, mỗi giá trị góp mặt ba lần. Ngoài ra có hai giá trị lần lượt là 0, 1 cũng đáng lưu ý.
- Dựa vào tính đối xứng, dữ liệu của bảng B có giá trị trung bình là 2.5. Tuy nhiên, các giá trị này lại trải ra rộng và đều, cụ thể nếu như bảng A có hai điểm tương đối xa trung tâm là 0, 1; thì bảng B có sáu giá trị như vậy (ba số 0, ba số 5).
Kết luận: Từ nhận xét trên, A là đáp án chính xác.
Một cách ngắn gọn hơn, ta thấy các giá trị của bảng A co cụm hơn bảng B, nơi mà các giá trị được trải đều.
Ví dụ 2.6:
| Data set P | Data set Q | |||
| Value | Frequency | Value | Frequency | |
| 0 | 1 | 4 | 1 | |
| 1 | 1 | 5 | 1 | |
| 2 | 2 | 6 | 2 | |
| 3 | 3 | 7 | 3 | |
| 4 | 6 | 8 | 6 | |
| 5 | 5 | 9 | 5 | |
| 6 | 4 | 10 | 4 | |
| 7 | 3 | 11 | 3 | |
| 8 | 3 | 12 | 3 | |
| 9 | 2 | 13 | 2 | |
Compare the standard deviations of the two data sets shown.
Hướng dẫn:
– Thật khó để có một hình dung trực quan về “độ rộng” của các bộ giá trị này, bởi số giá trị là tương đối nhiều, các giá trị nằm trên một khoảng khá lớn, và trên hết chúng không được biểu thị dưới dạng hình ảnh trực tiếp. Để khắc phục hạn chế thứ ba, đơn giản ta có thể tự vẽ hai biểu đồ tần số dạng điểm đại diện cho hai bộ dữ liệu trên. Đừng lo lắng về việc các giá trị chạy trên các khoảng khác nhau, từ 0-9 đối với bảng P và từ 4-13 đối với bảng Q, bởi ta mong muốn đánh giá khoảng cách giữa các giá trị thay vì bản thân độ lớn của chúng.
Chẳng hạn, khoảng cách giữa 0-2 và khoảng cách giữa 98-100 là như nhau. Do đó, điều quan trọng khi vẽ biểu đồ chấm để mô phỏng lại hai bảng trên là dãn cách các mốc theo đúng tỉ lệ, ví dụ 1 đơn vị là 1cm – tham khảo các ví dụ trên)
– Có một điểm đặc biệt cần lưu ý đối với hai bảng trong bài này, đó là các giá trị của bảng Q thực chất chỉ là giá trị “tương ứng” của bảng P tịnh tiến lên 4 đơn vị (cộng thêm 4). Do đó, với nhận xét ở trên rằng điều quan trọng không phải bản thân giá trị của các điểm, mà là khoảng cách giữa chúng, ta khẳng định rằng độ lệch chuẩn của hai bảng là bằng nhau.
Bình luận:
– Để minh hoạ cho lập luận trên, ta có thể quan sát bảng sau:
Đây không phải hình vẽ chính xác của dữ liệu ở hai bảng đã cho, nhưng qua đó ta nhận thấy cơ sở của khẳng định vừa nêu.
– Nếu muốn chắc chắn hơn nữa, bạn hãy tính tường minh độ lệch chuẩn ứng với từng bảng giá trị.
Ví dụ:
Data set A consists of 20 different values that have a minimum of 22, a maximum of 86, and a mean of 54. The values 22 and 86 are removed from data set A to create data set B, which consists of 18 different values. Compare the standard deviations of data set A and data set B.
Hướng dẫn:
Ở đây ta không có quá nhiều dữ kiện để làm việc cùng, nên ta cần sử dụng hiệu quả những gì mình có.
- Ta thấy hai số được bỏ khỏi tập A, 22 và 86, có trung bình cộng bằng 54. Kết hợp điều này với giả thiết tập A có giá trị trung bình đúng bằng 54, ta suy ra giá trị trung bình của tập B cũng vậy.
- Đề bài cho 22 và 86 lần lượt là hai giá trị nhỏ nhất và lớn nhất của tập A. Do đó, trên trục số, khi xét hai tập A, B có cùng giá trị trung bình, tập B được bớt đi được hai điểm nằm xa nhất về hai phía sẽ có độ lệch chuẩn nhỏ hơn.
Trên đây là một số ví dụ để minh họa cách thức đánh giá độ lệch chuẩn qua những câu hỏi của SAT Toán. Điều quan trọng để làm tốt dạng bài này trong đề là hình dung, nhận diện một cách trực quan một độ lệch chuẩn “lớn” hay “nhỏ”. Các quy tắc cơ bản đã được khái quát và bàn luận đôi chút trong bài viết. Song, chỉ thông qua luyện tập, tích lũy kinh nghiệm thì ta mới vận dụng được chúng một cách chủ động và phù hợp với bản thân.
Cùng Phoenix Prep xóa tan mọi trở ngại để HỌC GỌN GÀNG, THI XUẤT SẮC!
__________________________________
Phoenix Prep – Elevating Futures: High SAT & IELTS Scores Define Us
Hotline: 0836.575.599 (Ms. Hằng)
Sĩ số lớp: 7-10 học viên